| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- IDE #spyder
- Chap4 #다항회귀 #PolynomialRegression #ML #머신러닝
- 핸즈온머신러닝 #handson
- python #dataframe #파생변수 #map #lambda #mapping
- 티스토리블로그 #티스토리 #PDF #블로그PDF저장
- Chap4 #릿지회귀 #정규방정식 #확률적경사하강법 #SGD #규제가있는선형모델
- 인덱싱 #슬라이싱 #python #파이썬 #수정및삭제 #원소의수정 #객체의함수 #keys#values#items#get#len#append#sort#sorted
- 선형회귀 #정규방정식 #계산복잡도 #LinearRegression #Python #ML
- python #파이썬 #pandas #dataframe #dataframe생성 #valueerror
- ML #핸즈온머신러닝 #학습곡선 #편향분산트레이드오프
- 객체의종류 #리스트 #튜플 #딕셔너리 #집합 #Python #파이썬 #list #tuple #dictionary #set
- 티스토리 #수학수식 #수학수식입력 #티스토리블로그 #수식입력
- Chap4
- 확률적경사하강법 #경사하강법 #머신러닝 #선형회귀 #ML #Chap4
- adp #데이터분석전문가 #데이터분석자격증 #adp후기 #adp필기
- Chap4 #ML #미니배치경사하강법 #경사하강법 #머신러닝 #핸즈온머신러닝
- 파이썬 #Python #가상환경 #anaconda #python설치 #python가상환경
- Chap4 #핸즈온머신러닝 #머신러닝 #핸즈온머신러닝연습문제
- 경사하강법 #핸즈온머신러닝 #머신러닝 #ML
- 라쏘회귀 #엘라스틱넷 #조기종료
- 키워드추출 #그래프기반순위알고리즘 #RandomSurferModel #MarcovChain #TextRank #TopicRank #EmbedRank
- Chap4 #ML #배치경사하강법 #경사하강법 #핸즈온머신러닝 #핸즈온
- Today
- Total
StudyStudyStudyEveryday
1-1. 기계학습 간단 정리 - 모형의 적합 본문
1. 모형의 적합
1-1. 선형회귀모형의 적합
1-2. 분류모형의 적합
1-3. 군집모형의 적합
1-4. 손실함수와 위험
1-1. 선형회귀모형의 적합
선형 회귀모형
: 반응변수 y와 한개 이상의 설명변수 x의 선형 관계를 모델링하는 회귀분석 방법
모형식은 다음과 같다.

- \(\beta_{0}\)를 intercept, \(\beta_{j} (j\geq 1)\)를 regression coefficients라고 부른다.
- 이 intercept와 regression coefficients를 데이터로 부터 추정하는 것이 목표이며, 이것을 선형회귀모형의 모형적합이라 한다.
- 여기서 y가 예측값(실수값)이고, x는 실수벡터이다.
예를 들어, 지역별 1000명당 범죄 건수로 정의한 범죄율(y)과 지역별 주거지 방의 평균 (\(x_{1}\)), 지역별 1940년 이전에 건축된 주택의 비율 (\(x_{2}\)) 간의 관계 분석이 있다.
행렬표현식은 다음과 같다.
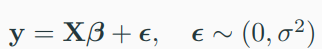

조건부 기대값과 모형의 의미
모형의 의미 : 설명변수가 주어진 경우 반응변수의 평균이 \(X\beta\) 이다.


위 그래프에서 조건부 평균을 이으면 선형이 된다.
최소제곱법을 이용한 회귀계수의 추정
최소제곱법 : 회귀모형의 회귀계수를 추정하는 방법 중 하나로, 모형의 적합값과 참값의 차이의 제곱합을 최소로 하는 추정 방법

여기서 \( \hat{y}_{i} = x^{T}_{i}\beta \) 이다.

추정모형을 이용한 예측
데이터가 주어진 경우, 최소제곱법을 통해 회귀계수를 구할 수 있다.
- 이미 관찰한 데이터로 예측 모형이 어떻게 설명하는지 확인
- 미래의 관찰하지 못한 데이터로 예측 모형이 어떻게 예측하는지 확인
=> 예측력을 어떻게 계산할까?
1-2. 분류모형의 적합
이진 분류 모형
: 반응변수 y가 두 개의 집단 변수(class variable)로 주어질 때, 관측치의 집단을 분류하기 위한 모형
- 손실함수는 관측치와 예측치의 일치/불일치 여부는 0과 1로 계산하는 0-1 손실함수를 흔히 사용
- Zero-one loss (0-1 loss)를 이용한 n개 데이터에 대한 위험 (risk)

여기서 예측치는 설명변수 x를 반응변수 y로 대응시켜주는 함수 C를 어떻게 결정하는지에 의존한다.
이진 분류에서 베이즈 의사결정경계
데이터가 iid 가정을 따르고 무한히 많으면 적합한 모형 C에 대한 합리적인 위험함수는 다음과 같다.

베이즈 최적의사결정 방법은 다음과 같다.

- \( P(y|x) \)를 알면 항상 가장 좋은 의사결정 가능
- 하지만, \( P(y|x) \)는 대부분 데이터로 부터 추론해야하기 때문에 이진분류를 위해서는 \( P(y|x) < 0.5 \)인 영역만 알면 됨
이진 분류모형의 위험함수
분류문제 : 위험함수를 최소화하는 C를 찾는 문제
- 추정값 \( \hat(y)_{i} \)에 대해 불연속함수인 0-1 손실함수 대신 연속함수인 Binary cross-entropy는 모형적합에서 계산상 얻는 이점이 커서 실제 데이터 분석에 많이 사용한다.

로지스틱 회귀모형
- 적합은 Binary cross-entropy 사용 (최대우도추정량)
- 결정경계를 기준으로 0 or 1 예측
- 적합값과 참값을 이용하여 분류모형 해석 및 평가 (ACC, AUC 등)
1-3. 군집모형의 적합
다변량 혼합분포 모형
GMM (Gaussian mixture model) : K개의 다변량 정규분포의 결합으로 이루어진 혼합모형

- 위 pdf에서 \( \pi_{k} \) 는 weight, \( N(x|\mu_{k}, \Sigma_{k}) \)는 다변량 정규분포이다.
- 모형기반 군집방법 (정규분포)
- 군집을 몇 개의 모수로 표현 가능하다.
- 서로 다른 크기/모양을 가지는 군집을 찾을 수 있다.

다변량 혼합분포 모형 적합 - 최대우도 추정방법 (Maximum Likelihood Estimation, MLE)
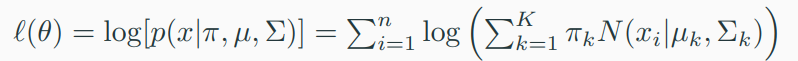
- 위 우도 함수를 \( \pi, \mu , \Sigma \)에 대해 각각 편미분 후 로그우도함수를 최대화하는 추정량 \( \theta_{k} , k = 1, \cdots , K\) 구하기
- 최대우도함수를 직접 최대화하는 방법은 국소최적해가 많아 계산에 매우 불안정
다변량 혼합분포 모형 적합 - EM 알고리즘

- E-Step과 M-step을 특정 횟수만큼 반복하거나 수렴하기까지 반복하는 방법이다.
- 계산의 안정성을 확보함 (가장 큰 장점)
- 매 반복마다 목적함수 (우도함수)가 단조증가한다는 장점이 있다. (Ascent property)
1-4. 손실함수와 위험
손실함수와 위험
기계학습의 모형적합은 대부분 목적함수의 최적화문제
- 손실함수 (Loss function)
- \( L(y_{i}, f(x_{i})) \)
- 데이터의 참값과 예측값의 차이를 수치화하는 함수
- 손실함수 특성(미분가능성, 볼록함수 등)에 따라 모형적합 과정이 다양한다.
- ex) hinge loss, 0-1 loss, cross-entropy loss 등
- 위험함수 (Risk function) ★
- \( R(f) = E[ L(y_{i}, f(x_{i})) ] \)
- 손실의 기대값을 의미
경험적 위험함수와 모형의 제약

경험적 위험함수 (Empirical risk function)

- loss의 표본으로 정의된 것을 이용한다. (마치 모평균 - 표본평균 같은 의미)
- n개의 데이터 손실의 평균 의미
- 데이터가 iid를 따를 때 경험적 위험함수는 \( R(f) \)의 극한이므로 \( R(f) \)의 근사값으로 해석하기도 한다.
볼록최적화 알고리즘 계산
- 볼록최적화 (Convex optimization) : 목적함수가 볼록함수인 최적화 문제
- Standard form
- 여기서 x는 model parameter, f(x)는 경험적 위험함수이다.
- 아래는 model의 제약조건

- 경사하강법 (Gradient Descent, GD) : 최소 초기값 설정 후, gradient vector 값을 구해 최적해를 점진적으로 찾아가는 방법 ( 링크 참고 )
신경망 모형과 모형적합을 위한 최적화

- 다양한 예측/분류 모형 적합
- 오차역전파법(Backpropagation) ★ 활용 : 실제값과 신경망 모델로부터 계산된 값 사이의 오차를 역순으로 전파하여 그 오차를 줄여가는 알고리즘 ( Gradient 계산에서 합성함수 미분 시 발생하는 중복계산을 줄인 효율적인 경사하강법)
'DataScience > 비정형 데이터 분석 (빅데이터와 통계읽기)' 카테고리의 다른 글
| 1-2. 기계학습 간단 정리 - 모형의 평가 (0) | 2022.04.11 |
|---|

