| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 경사하강법 #핸즈온머신러닝 #머신러닝 #ML
- Chap4 #다항회귀 #PolynomialRegression #ML #머신러닝
- IDE #spyder
- adp #데이터분석전문가 #데이터분석자격증 #adp후기 #adp필기
- 라쏘회귀 #엘라스틱넷 #조기종료
- Chap4 #핸즈온머신러닝 #머신러닝 #핸즈온머신러닝연습문제
- Chap4 #릿지회귀 #정규방정식 #확률적경사하강법 #SGD #규제가있는선형모델
- python #dataframe #파생변수 #map #lambda #mapping
- Chap4 #ML #미니배치경사하강법 #경사하강법 #머신러닝 #핸즈온머신러닝
- 키워드추출 #그래프기반순위알고리즘 #RandomSurferModel #MarcovChain #TextRank #TopicRank #EmbedRank
- 인덱싱 #슬라이싱 #python #파이썬 #수정및삭제 #원소의수정 #객체의함수 #keys#values#items#get#len#append#sort#sorted
- Chap4 #ML #배치경사하강법 #경사하강법 #핸즈온머신러닝 #핸즈온
- Chap4
- ML #핸즈온머신러닝 #학습곡선 #편향분산트레이드오프
- 티스토리 #수학수식 #수학수식입력 #티스토리블로그 #수식입력
- 파이썬 #Python #가상환경 #anaconda #python설치 #python가상환경
- 선형회귀 #정규방정식 #계산복잡도 #LinearRegression #Python #ML
- 객체의종류 #리스트 #튜플 #딕셔너리 #집합 #Python #파이썬 #list #tuple #dictionary #set
- 티스토리블로그 #티스토리 #PDF #블로그PDF저장
- 확률적경사하강법 #경사하강법 #머신러닝 #선형회귀 #ML #Chap4
- 핸즈온머신러닝 #handson
- python #파이썬 #pandas #dataframe #dataframe생성 #valueerror
- Today
- Total
StudyStudyStudyEveryday
머신러닝 모델 훈련 - 경사하강법(Gradient Descent, GD) 본문
경사하강법
경사 하강법 (Gradient Descent, GD)은 여러 종류의 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화 알고리즘이다. 경사 하강법은 비용함수를 줄이기 위해 반복해서 파라미터를 조정해간다.
첫 시작은 파라미터 벡터 \(\mathbf{\theta}\)를 임의값으로 설정하여 시작한다. (무작위 초기화 random initialization) 그 다음, \(\mathbf{\theta}\)에 대해 비용함수(예를 들어 MSE)의 현재 Gradient를 계산한다. 그리고 Gradient가 감소하는 방향으로 파라미터를 조정해나간다. 이를 반복하여 Gradient가 0이 되면 최솟값에 도달한 것이다.
* 여기서 Gradient는 비용 함수의 미분값이라고 생각하면 된다.
즉, 정리해보면 다음과 같다.
- 무작위로 임의의 초기값 \(\mathbf{\theta}\) 설정
- \(\mathbf{\theta}\)에 대해 비용함수의 현재 Gradient 계산
- 비용함수가 감소되는 방향으로 파라미터 조정
- Gradient가 0이 되면 반복 중지
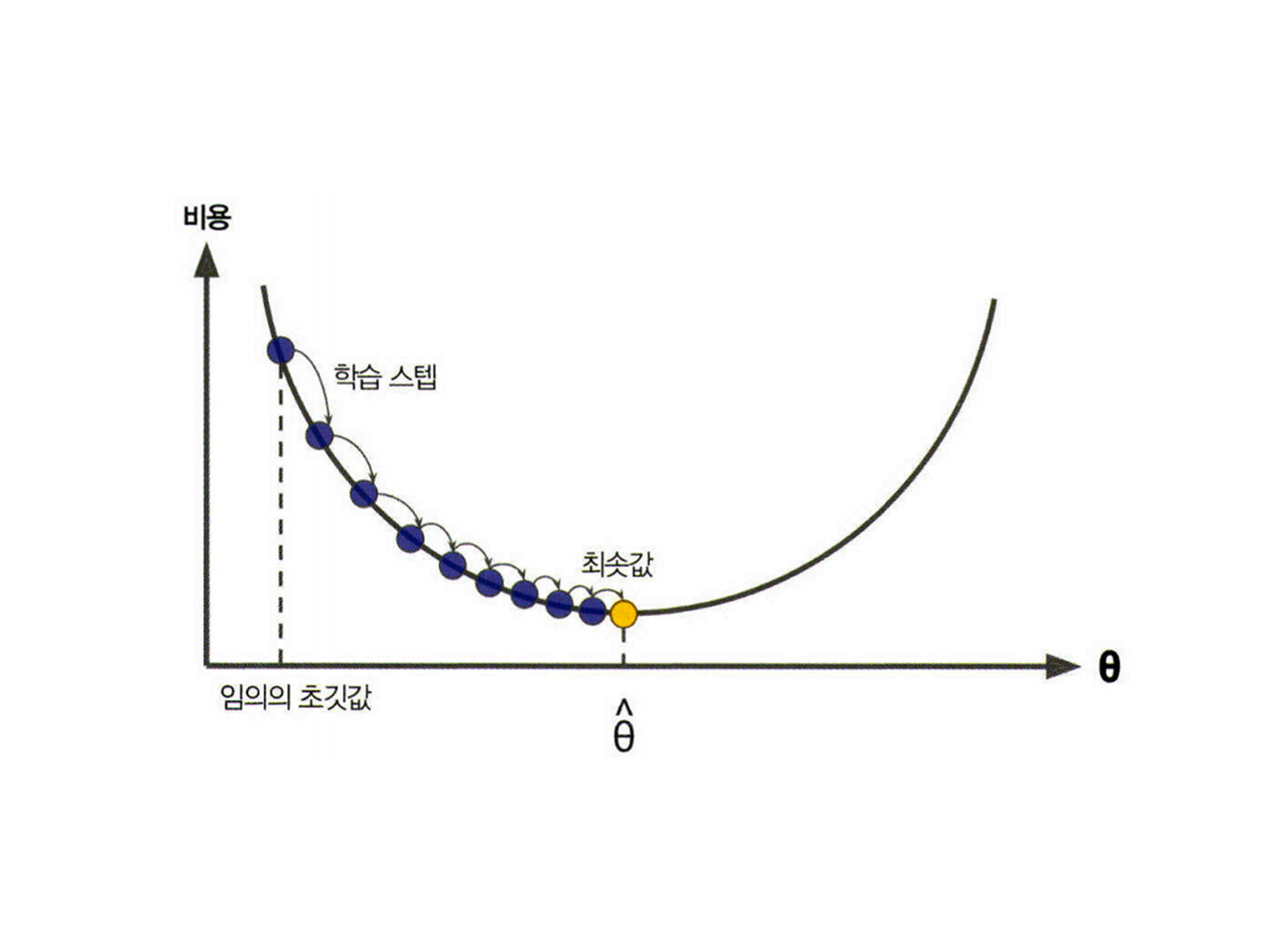
여기서 학습 스텝(Learning step)의 크기는 비용 함수의 기울기에 비례한다. 따라서, 파라미터가 최솟값에 가까워질수록 스텝 크기가 점진적으로 줄어든다.
경사하강법의 문제점
학습률이 수렴 속도에 영향을 끼친다
경사하강법에서 중요한 파라미터는 스텝의 크기로, 학습률(learning rate) 하이퍼파라미터로 결정된다. 학습률이 너무 작으면 알고리즘 수렴까지 반복이 많이 되어야하므로 시간이 오래걸린다. 반면, 학습률이 너무 크면 학습 이전보다 기울기가 더 높은 곳으로 발산하게 만들 수도 있다.


비용 함수의 지형에 따라 전역 최솟값에 도달하지 못할 수 있다
위의 경우는 변곡점(골짜기)이 하나만 있는 단순한 형태의 비용함수이다. 하지만, 패인 곳, 산마루, 평지 등 다양한 지형이 있는 비용함수의 경우 전역 최솟값(global minimum)보다 지역 최솟값(local minimum)으로 수렴해 우리가 원하는 전역 최솟값으로 수렴하기가 어렵다.

선형 회귀를 위한 MSE 비용 함수는 볼록 함수이므로 지역최솟값이 없고 하나의 전역 최솟값만을 가진다. 또 연속적이고 기울기가 갑자기 변하지 않아 학습률이 너무 높지않고 충분한 시간이 주어진다면 경사하강법을 적절하게 활용할 수 있다.
특성 스케일에 따라 최솟값에 도달하는 시간이 오래 걸릴 수 있다

특성 스케일을 적용한 경사 하강법(왼쪽)의 경우 알고리즘이 최솟값으로 곧장 빠르게 진행되어 도달한다.
하지만, 특성 스케일을 적용하지 않은 경사 하강법(오른쪽)의 경우 일정 수준 학습을 하다 평편한 골짜기에 들어 돌아가게 된다.
따라서, 경사 하강법을 사용할 시에는 반드시 모든 특성이 같은 스케일을 갖도록 만들어야 한다.
(StandardScaler, MinMaxScaler 등 이용)
* 해당 포스팅은 머신러닝 학습 중 핸즈온 머신러닝 2판을 참고하여 작성하였습니다. *

'DataScience > 핸즈온 머신러닝 Hands-on ML' 카테고리의 다른 글
| 머신러닝 모델 - 다항 회귀 (Polynomial Regression) (0) | 2022.03.24 |
|---|---|
| 머신러닝 모델 훈련 - 미니배치 경사 하강법 (Mini-Batch Gradient Descent) | 세 가지 경사 하강법 비교 (0) | 2022.03.24 |
| 머신러닝 모델 훈련 - 확률적 경사 하강법 (Stochastic Gradient Descent, SGD) (0) | 2022.03.24 |
| 머신러닝 모델 훈련 - 배치 경사하강법(Batch Gradient Descent) (0) | 2022.03.24 |
| 머신러닝 모델 - 선형 회귀 (Linear Regression) (0) | 2022.03.24 |




